Some Deeper information about the LUNA Scales
Why the Luna is tuned in its own scales, and what`s the difference to common handpan scales?
About the perfect just intonation as given fom the natural overtone series, which the Luna tuned in.
About the Dominant or Subdominant Ding, what it is and whats special about its use ?
Why the Luna is tuned in its own scales.
About the LUNA Scales
The LUNA is built in 12 different "archetypes" or core scales.
Each of these 12 basic tunings is a associated to a mythological goddess.
A complete list of the 12 LUNA-tunings, can be found here and on my scales page.
Why the naming after goddesses and only 12 scales?
Since I have a personal fascination and great interest in the female entities & goddesses of the myths of old, I link to this inspiration with the LUNA-scales.
But there are also more reasons for this.
First of all, it is a response to the ever increasing confusion surrounding the subject of "Handpan Scales".
The feedback I receive from people who often have great problems to find and choose their Handpan scale reflects this confusion.
Many people without a background in music theory are simply overwhelmed by the multitude of different scale designations and sound models that exist for handpans, especially since there are many very similar moods where only e.g. only one tone differs - but which still have the same core character.
Furthermore, the names of common handpan scales, like the "Anna Ziska", the "C-Amara" or the "Kurd" are no music-theoretical "real" names - this would be for the Kurd and many others e.g. the so called "aeolian minor".
But what seems even more important to me personally is that they give no hint about the sound character, or the feeling, the "heart" of the mood.
Names like "Anna Ziska" "Kurd" or "Amara" do not indicate whether the mood is happy or cheerful, whether the mood is calm or lively - they are completely meaningless for people without any background in music theory.
And even for people with a background in music theory, the name says nothing about the interval characteristic or the gender of the sound.
For example, the name "C-Amara" simply says nothing about the mood, neither that it is an Aeolian minor, with classical minor ore, nor that it creates a slightly melancholic but nevertheless balanced mystical atmosphere or energy.
The 12 core scales of the LUNA - and the naming after the mythological goddesses and their archetypal associations is therefore an attempt to convey the "root" or "heart" of the different scales in a way that is understandable to everyone - in order to offer fewer, but better distinguishable and characteristically clear moods for the LUNA.
If you are faced with the challenge of having to decide on a handpan tuning, this association and naming can reduce a big hurdle.
Whoever deals with the mythological figure or goddess LILITH, or reads the descriptions and associations on my tuning sheet will immediately notice that the mood named after her must have a completely different character than the mood named after the goddess ANTHEIA.
For LILITH, in her role as Adam's first wife, who rebelled against her husband's dominance in paradise and - since she knew the "Word of Power" - could not be tamed even by God, has a much more dramatic role than ANTHEIA, the shy Greek goddess of plants and flowers, whose main trait is tenderness and her look and respect for even the smallest and most delicate flowers and beings.
The former symbolizes the urge for freedom - the courage and strength to rebel against hierarchies - even against the command of the highest God - and to follow one's own heart, which in the Abrahamic religions eventually led to their demonization and association with demonic forces.
The latter, on the other hand, symbolizes tenderness and the power of the small and weak, mindfulness and compassion.
Admittedly, the associations of moods with the goddesses are subjective and to a certain extent arbitrary and reflect only my own impressions and feelings. Someone else might not feel the same associations and would not agree with my attributions and designations - a subjectivity that I consciously accept.
Last but not least there is another important point why I build the LUNA only in my own moods, and this is the sound quality.
The LUNA tunings are all specially designed for the LUNA, the shell geometry, size, material and tuning style are all variables that influence the choice of scale, the placement of the start intervals, the tone field orientation relative to each other, etc.
For these reasons it is not possible (or should not be possible) to simply take over a certain scale as it is found on a handpan from any manufacturer and transfer it 1:1 to your own handpan without deeper consideration.
Are the LUNA Moods something new that you have invented?
Partly not partly yes.
Some of them are neither new nor invented, although they have been modulated in such a way that they can be built on the LUNA with the highest possible sound quality.
In fact, some of the LUNA tunings are very old tunings and ancient Greek modes, (Tonai) like Aeolian ("typical D minor", "kurd", "enigma" etc.) Lydian, Ionic Phrygian etc.
Another part of the LUNA scales, is not found in European music culture, but originate from Japanese / Chinese culture, and yet others are actually freely "invented", although this does not mean that this tuning, as an interval combination, did not occur somewhere else before.
So the LUNA tunings are nothing completely new - in the handpan world however a special feature.
Perfect just intonation as derived from the natural overtone-Series
One of the main features of the LUNA scales is the use of also pure intonation as opposed to the most commonly used modern midrange temperament.
This ensures that all intervals are tuned very clearly and purely and the internal resonance is significantly increased.
Although I will try to keep the explanation simple, we will have to dive a little into music theory to fully understand this:
First of all, we have to understand that scales are never defined by notes - they are defined by a certain combination of interval steps (which can then be represented by notes).
So what is an interval?
Well, let's pick any frequency as a fundamental - just imagine a plain string, like a guitar string or another. It doesn't matter how long this string is, but for simplicity's sake we assume it's 1 meter long.
So this is our basic frequency - or the tonic of our scale.

Imagine now, we take a finger and pluck this string - it will start to vibrate as follows (in reality it vibrates in many more ways, but these are irrelevant to us at first) and emit a tone.
Our fundamental - let's say it is a C3.

We can now define this frequency in a simple mathematical term as 1 or - we will need this later - as a ratio of 1/1 equal to 1.

Based on this, we now create our first interval step, which is one of the most important: the octave.
The octave sounds like exactly the same note - but a "step" above our foundation, and it has twice the vibration frequency as our fundamental.
On our string, the octave would fibrillate so and can be mathematically defined as the double frequency, tso 2 ( 2x1) or the ratio: 2/1

So now we have our base frequency, with the ratio 1/1, of which we said it was C3 (but it could be any other note) and we have our octave, which is the ratio 2/1 and thus a C4.
These are the limits within which we create a scale. Everything that goes above or below these octaves is just a repetition that we don't have to worry about now.
So let us take the second most important interval, which is the fifth.
The fifth is perceived as a very pleasant interval step and is so important that the entire Western 12-note system is based on it, namely on the quint-layering.
On our string, the fifth would vibrate as follows:
To make the fifth sound, we would have to shorten our string, for example, like a guitar player shortens a string when he picks it off with his finger.
This should be done in the ratio 3/2, which is the ratio of the pure fifth:
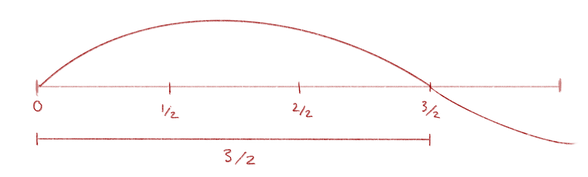
In our example of the C3, the fifth with the ratio 3/2 would be G4.
Starting from here, the chromatic scale of Western music was constructed, which places fifths on fifths.
So let's start from C and look for the fifth of it, the G.
If we repeat this step and look for the fifth to the G, we come to the D.
On the keyboard of the piano, we always move 7 semitones to the right.
We can also calculate the ratio of this D.
This is done simply by multiplying the G -> 3/2 by another fifth step, i.e. 3/2, and then going an octave lower.
It looks like this:
3/2 x 3/2 = 9/4
Now that we have exceeded the octave point, however, we must lower the result by one octave so that we are again within the correct octave and thus receive the D as the second after the C.
For this we have to divide the result by the ratio of the octave we said to be 2/1:
9/4: 2/1 = 9/4 x 1/2 = 9/8
The perfect D, as derived from the quint layering, would therefore have a ratio of 9/8.
In our drawing its oscillation would look like this:
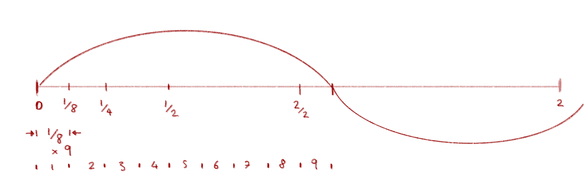
And here is how those frequencys would vibrate differently on our string:
the tonic - octave - fifth - the second ( wich we calculated as fifth from the fifth )

Now that we understand this, we can see how the 12 notes are created in Western music - they are all created as a fifth from the fifth from the fifth from the fifth from the fifth.... here is the complete series of fifths that begins with C, followed by the fifth of C = G followed by the fifth of G = D etc..
C -> G -> D -> D -> D -> A -> E -> E -> B -> Gb -> Db -> Ab -> Eb -> Eb -> Bb -> F -> C
That is why European music has 12 notes, because after 12 such operations you reach FAST - but only almost - the opening note, the C.
And this is where the problem and the various attempts to solve it, such as the mid-tone temperament, begin.
Mathematically speaking, the multiplication of fifths is always a multiple of 3/2.
Or, if we want to represent the ratio as a decimal number: 3/2 = 1.5 multiples of 1.5.
So we have multiples of 1.5 which we can also write as a superscript 1.5^2 ( 1.5 x 1.5).
The core problem is that we calculate with the ratio 2/1, i.e. with multiples of 2 ( 2^2 ; 2^3 ; 2^4 etc.) in order to get perfect octaves.
But unfortunately these two never fit together perfectly.
You can demonstrate this by looking at where a multiplication in octave steps ends after a complete octave:
Namely after 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2^7 (because we created 7 whole tones between one octave) = 128
And here ends the series of multiples of 1.5 ( thus the quint layering ) after 12 steps ( since we produce 12 semitones ):
1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 = 1,5 ^12 = 129,75
So we have the result 128 once and 129.75 once.
As we can see, perfect octaves can never be matched with perfect fifths or interval steps. It seems that we have to decide... perfect octave or perfect intervals...
What are the solutions?
Well, great thinkers have been thinking about it for centuries, starting with one of the first, Pythagoras, but also Kirnberger, Bach and many other musicians and composers have developed their own suggestions and methods to solve this problem.
At the moment we will not go into these like e.g. the Pythagorean tuning or others.
Suffice it to say that there are hundreds of different temperaments and tuning methods. ( Alone in Europe - not to mention completely different methods in different cultures! )
The most common type of tuning today to deal with this problem is the so-called mid-tone tempering, which is also the widespread standard for Handpans.
We have seen that we end with multiples of perfect fifths at 129.75, while the perfect octave ends at 128.
The difference between these two is the so-called "Pythagorean comma" which is calculated as follows: 129.75 - 128 = 1.75
This difference would produce an audible dissonance in the last interval step, or - with perfect intervals - make the octave appear clearly too high.
The mid-tone tempering deals with this problem as follows:
We take the Pythagorean comma - 1.75 and divide it by 12 - because we have 12 interval steps - and then distribute this error evenly over all intervals.
So 1.75 : 12 = 0.145 on each of the 12 interval steps to achieve a perfect octave.
This means, for example, if the perfect ratio of e.g. a fifth is 3/2 = 1.5 in the pure tuning.
then it is now 1,645 in the mid-tone temperament.
A mid-tone fifth is therefore slightly higher and slightly out of tune, in contrast to a pure, perfect fifth.
Another example based on the fourth:
The ratio of a perfect fourth 4/3 = 1,333
The ratio of a mid-tone quarter = 1.478
To sum up: The Western mid-tone temperament has only one single, truly natural and pure interval, the octave.
All other intervals must be somewhat impure and out of tune to fit the octave at the end.
Even if the difference seems to be tiny (e.g. from 1.5 to 1.645 for the fifth), it is perceptible to an experienced ear and gives the intervals and especially the chords a restless, impure quality.
So far so good. But if the LUNA is tuned purely, then it doesn't fit the octave at the end, does it?
Yes she does.
The LUNA contains perfect natural octaves in a 2/1 ratio, just like the mid-tone temperament, AND has the perfect intervals in perfect natural ratios, like 3/2 - 4/3 etc.
Since the Handpan is not a chromatic instrument with all 12 semitones, it opens up a special possibility for pure tuning.
For every LUNA tuning there is a certain mathematical calculation in which the "error interval", also called "Wolf's fifth", is mathematically "compressed" and calculated into a note that simply does not occur in the respective scale!
The mathematical error, the non-matching of fifth and octave multiples is shifted until it comes to rest in an interval that does not exist on the instrument.
This must be calculated individually for each individual scale on the LUNA tuning list.
Again summarized in a few words: All LUNA scales are in pure, natural, perfect intonation. They have both perfect interval steps and perfect octaves, because the Pythagorean comma is calculated for each individual scale so that it does not appear on the instrument.
It is not just a mathematical gimmick, because the pure tuning is also naturally perceived by the ear as pure tuning, compared e.g. with the mid-tone temperament.
This is the most natural and cleanest tuning possible in the non-chromatic range.
Tonal, Subdominant or dominant Ding and full range of Scale
Basically, hand pans can always be played in two different ways, namely Ding - centered or chorus centered with dominant or subdominant thing.
What do "tonal", "dominant" and "subdominant" mean?
1. tonal Ding
A tonal Ding means that the ding is set equal to the fundamental note of the tuning. It is therefore the centre of all melodies played in the chorus and all melodies find their resolution and their resting place in the Ding.
This is the most common way of playing handpans, but it carries with it the potential for a certain monotony.
2. dominant Ding.
A dominant Ding means that the tonic of the scale is the fifth of the Ding. ( Or in other words, the thing is the fourth of the fundamental. )
For example, with a G3 this would be the C3. ( Since G3 is the fifth of C3. )
3. subdominant Ding.
This means that the Ding is the fifth of the fundamental ( tonic ), but is located one octave lower - for a G3 as fundamental, D4 is the dominant ( fifth ) - subdominant would then be a D3.
What is the difference between subdominant, dominant and a tonal Ding?
While in most handpans the Ding is always played as the tonic, i.e. the keynote, the LUNA and its tunings invite you to play the Ding also dominant or subdominant.
Why?
The typical tuning and use of the Ding as the keynote of the instrument means for example a C3 Ding for a C scale, e.g. the C-Amara or a D3 Ding for a D scale like D minor or D Kurd.
This reflects the typical style of playing for handpans that has developed and established itself in recent years, with a strong focus on percussive patterns.
As the Handpan became available to a wider public, it attracted many people with percussive backgrounds, drummers, darbouka players and other percussionists.
They took what they brought from their percussive background and applied it to the handpan.
This resulted in a way of playing that was largely focused on percussive patterns, which is one possible way of dealing with this instrument and will not be criticized here, but it is not the only way to approach this instrument.
It is only natural that from this perspective the Ding plays a very dominant and important role in the playing technique of most handpan players, while the chorus (the notes in the ring) plays a somewhat subordinate role and is often only used in a way to fill the rhythmic patterns.
The LUNA, however, was conceived from its beginnings as a more melodic instrument with a much more "feminine" character.
For an instrument with this focus, however, the keynote-Ding interpretation is not always the only sensible one for the following reasons:
One problem may be that on most tonal Ding scales, the first note field of the instrument is NOT the fundamental of the scale.
With a tonic thing, the scale usually begins somewhere in the middle, usually the 3rd or 4th, sometimes even higher tone field, as is the case with the so-called D-Minor or Kurd, which has a D3 in the Ding - and which only continues the chorus with its fifth, the A3. ( D ) A - Bb - C - D - E - F - G - A - C )
This results in a split scale where the lower part is not complete and is shifted to the upper part above the octave. This makes it impossible to play complete melodies in this scale, because the scale is simply not completely available between one octave and the next.
As a result, although certain musical scales can be called tonic Ding scales, they practically cannot be played melodically in this key, which leads to great confusion.
In my opinion, one of the main reasons for this inability to play complete melodies in the mode is the inability to play complete melodies, which in my opinion leads to a strongly Ding-centered, percussive playing style, with more or less hard beats and repeated beats on the Ding, accompanied by only a few melodic accents.
This is the current development direction of the handpan.
An interpretation with a subdominant or dominant Ding, on the other hand, offers a complete scale from the first tone field with tonic to the last with octave, which invites a much more melodic approach to the instrument.
Depending on the interval structure of the scale, dominant and subdominant or tonal Ding playing styles have very different influences on the whole scale and can be used powerfully to emphasize the overall atmosphere and energy of a scale while allowing enough room for modal shifts.
In summary, while providing a definite centre of rest, both dominant and subdominant Dings inspire the player to focus more on the chorus and melodic play, as opposed to the typical percussive Ding-centric play that is more encouraged when the Ding is interpreted as the root note.
The claim of LUNA is to offer the best possible combination of aesthetics and musical possibility.
It is therefore built exclusively with a central note and 8 tone fields. No mutants, no 10 or 11 notes, no ground notes.
For me personally and from an aesthetic point of view, the Handpan in this format is at the height of elegance -
nothing can be added to it without taking away something of its minimalist form and elegance.
This is not to say that mutants, "bottomnotes" and other things are bad, there have been some LUNAE with such additional developments in the past, but it is not what I want to develop further.
Instead of adding more and new things, the Luna is an attempt to use my energy to see how far this simple elegance can be refined, polished and perfected.
This decision also influences the choice of the tuning of the Ding - because if the basic tone is on the first tone field and not on the thing, the whole handpan gets another layer of playing possibility by just this fact, which is very important if you are limited to a central tone field and 8 more tone fields.
In some scales this also gives you an additional note by the fifth of the Ding tone field, which is not necessarily in the chorus, so that you get the maximum possible musical expression on the most elegant and minimal design - the goal of the LUNA.
